HOW TO READ LARGE NUMBERS

Numbers are separated into groups: ones, tens, hundreds, thousands, millions, and so on. Each group contains three subgroups: ones, tens, and hundreds. When writing or reading a large number, begin at the left with the largest group, and proceed to the right. For instance, 7,482 is read as seven thousand, four hundred, eighty-two. The following chart can help in reading large numbers.
 

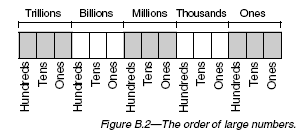
Example 1 - How do you read 10,956,501? 
 

The answer is: ten million, nine hundred fifty-six thousand, five hundred, one.

ADDITION: ADDING TO A SUM OR TOTAL

Addition is used when combining items, or putting items together to obtain a total. It helps answer questions such as "How many?" "How much?" or "How far?" Let's look at different ways that addition can be used. Some words used often to refer to addition are "plus", "and", "the sum of", "total", or "added to".

Example 1 - Pedro's crew has 4 pulaskis. Jane's crew has 6 pulaskis. How many pulaskis do they have together?

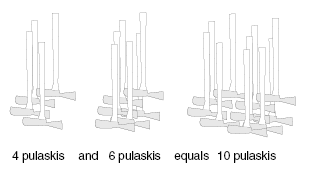
As shown the the figure above, the addition needed to answer this question is: 4 + 6 = 10.
 

ADDITION IS USED IN COMBINING DISTANCES OR LENGTHS.

Example 2 - Crew 1 constructs 14 chains of handline on the day shift. Crew 2 constructs 11 chains of handline on the night shift. How many chains did crew 1 and 2 construct altogether?

14 chains + 11 chains = 25 chains

 

ADDITION IS USED TO FIND THE DISTANCE AROUND AN OBJECT.

The total distance around an object is called the perimeter.

Example 3 - The Division Supervisor (DIVS) used two dozers to construct a line. The dozers cleared a line of the following shape. How many chains of dozer line were constructed?
 

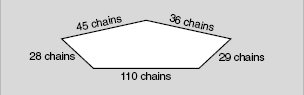
45 chains + 36 chains + 28 chains + 29 chains + 110 chains = 248 chains

 

ADDITION IS USED IN COMBINING AREAS.

Example 4 - The day shift had two spot fires that were contained at 6 acres and 8 acres each. What was the total area of the spot fires that burned during the day shift?

6 acres + 8 acres = 14 acres

 

ADDITION IS USED IN COMBINING VOLUMES.

Example 5 - Herman pumped 30 gallons of fuel into one tank, 25 gallons into the next tank, and 27 gallons into the last tank. How many gallons of fuel did Herman pump?

30 gallons + 25 gallons + 27 gallons = 82 gallons

 

ADDITION IS USED IN COMBINING LARGER NUMBERS.

When adding several numbers, especially large numbers, add the ones (1s) first, then the tens (10s), then the hundreds (100s), and so on.

Example 6 - Add: 548 + 365
First, add the ones. There are 13 ones, or 1 ten and 3 ones. Write 3 in the ones column and "carry over" the 1 above the tens.
Next, add the tens. There are 11 tens, or 1 hundred and 1 ten. Write 1 in the tens column and the 1 above the hundreds.
Now, add the hundreds. There are 9 hundreds.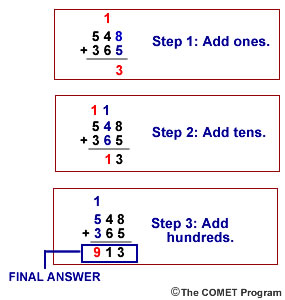
The answer to 548 + 365 is 913.

ADDING POSITIVE AND NEGATIVE NUMBERS

Numbers can be positive or negative. Positive numbers are indicated with a + sign, or have no sign. If a number is written without a sign, the sign is assumed to be positive. Negative numbers are indicated with a - sign. For example, a negative pressure may be indicated as -25 inches of Hg, or as a vacuum of 25 inches of Hg. 

Signs are important in adding numbers. Here are some easy rules to help determine the sign of a sum: 

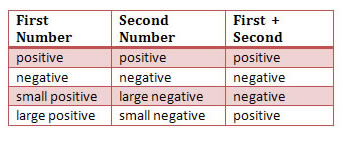
Example 7 - Adding numbers with like signs.
5 + 5 = 10
3 + 3 = 6
-5 + (-5) = -10
-3 + (-3) = -6
 

Example 8 - Adding numbers with unlike signs. Notice that the sign of the larger number is the sign that the answer will have.
5 + (-3) = 2
3 + (-3) = 0
3 + (-5) = -2
2 + (-3) = -1

SUBTRACTION: COMPUTING A DIFFERENCE

Subtraction is used in two types of situations. The first is "How much is left?" and the second is "How much more is needed?" Some words used in subtraction are "minus", "take away", "less", and "difference".

Example 1 - How many are left? 
 

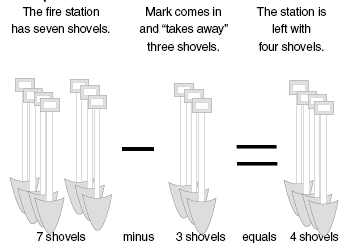
In the figure above, the fire station has 7 shovels. Mark "takes away" 3 shovels. How many shovels are left? 

Set up the problem as 7 shovels minus 3 shovels. The answer to 7 - 3 is 4 shovels.

SUBTRACTING LARGE NUMBERS

Example 2 - Subtracting numbers. Subtract 5342 from 9854.

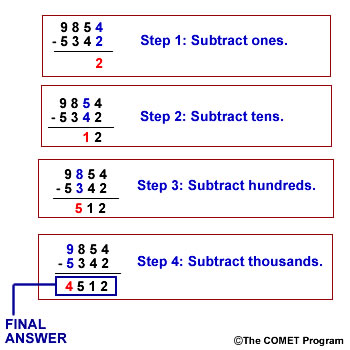
As shown in the example above, first subtract the ones. Next, subtract the tens. Keeping moving from right to left, so next subtract the hundreds, and finally, subtract the thousands.
The answer to 9854 - 5342 is 4512.

"BORROWING" NUMBERS

As you subtract numbers in the ones, tens, hundreds, etc. position, you might find that the number being subtracted is larger than the one from which you are subtracting. In this case, "borrowing" from the next column to the left is necessary.

Example 3 - Subtract 932 minus 784.

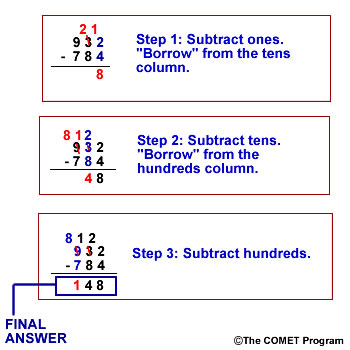
First, subtract the number in the ones column. Because 4 cannot be taken away from 2, 1 ten must be borrowed to get 12 ones. Now take away 4 from 12 to get 8.
Move to the tens column. Because 8 cannot be taken away from 2, borrow 1 hundred to get 12 tens, and take away 8 from 12 to get 4.
Finally, we move to the hundreds column. There are 8 hundreds left and we will take away 7 to get 1. 
The answer to 932 - 784 is 148.

SUBTRACTING SIGNED NUMBERS

Signs are important in subtracting numbers. Subtracting a negative number changes the sign of the number subtracted. When subtracting a negative number, the subtraction sign and negative sign together produce a positive number. Subtracting a negative number therefore has the result of adding a positive number. See the examples below.

7 - (-3) = ? becomes 7 + 3 = 10.
50 - (-20) = ? becomes 50 + 20 = 70
84 - (+26) = ? becomes 84 - 26 = 58
192 - (-301) = ? becomes 192 + 301 = 493
-50 - (-20) = ? becomes -50 + 20 = -30 
In the last case, because a larger negative number (-50) was added to a smaller positive number (20), the end result was negative. See Chapter 1, Section 1.2 for more information on adding numbers of different signs.

MULTIPLICATION: A SHORTCUT TO REPEATED ADDITION

Multiplication is a simpler way of doing repeated addition. Suppose Ron can do 30 push-ups in one minute. If he maintained a steady pace, how many push-ups could he do in five minutes? You could add 30 + 30 + 30 + 30 + 30, or you could multiply 30 × 5 to arrive at the answer of 150 push-ups. Some words and symbols used in multiplication are times, the product of, the "×" sign, or a dot like "•". Sometimes numbers that are being multiplied will be put in parentheses (30)(5)=150. 

Example 1 - Each person on your six-person crew is carrying five quarts of water. How many quarts of water does your crew have in total? 




The multiplication problem would be 5 × 6 = 30.
This process is the same as adding 5 six times.

When larger numbers are involved, multiplication is much easier than the repeated addition.

Example 2 - Multiply 17 by 63.

 

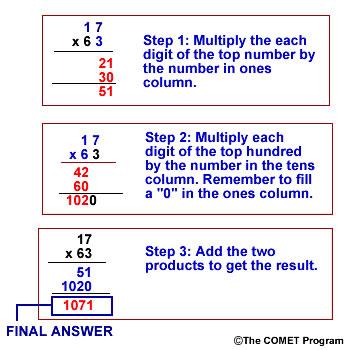
Step 1. Multiply the top number by the number in the ones spot, which is 3.
17 × 3 = 51

Step 2. Multiply by the number in the tens spot, or 60, by putting a "0" in the ones place and multiplying 17 × 6.
17 × 60 = 1020

Step 3. Add these together.
17 × 63 = 51 + 1020 = 1071

Example 3 - Multiply 374 × 261.

Follow the same steps as shown above.

Step 1. Multiply 374 by 1.

Step 2. Multiply by 60. Put a "0" in the ones place and then multiply 374 by 6.

Step 3. Multiply by 200. Put "0" in the ones and tens places and then multiply 374 by 2.

Step 4. Add the numbers. 
374 + 22,440 + 74,800 = 97,614


The answer to 374 × 261 is 97,614. 
 

MULTIPLYING SIGNED NUMBERS

When multiplying two numbers with the same sign, the answer will be a positive number. A positive number times a positive number always gives a positive answer.
5 × 5 = 25
4 × 8 = 32
2 × 6 = 12

A negative number times a negative number always gives a positive answer.
-5 × (-5) = 25
-5 × (-10) = 50
-9 × (-7) = 63

A positive number times a negative number always gives a negative answer.
5 × (-5) = -25
-70 × 8 = -560
24 × (-2) = -48

DIVISION: DIVIDING INTO SMALLER PARTS

Division is used to split groups up into smaller sections. Suppose there are 24 pairs of gloves in the storage locker and you want to distribute them evenly among 8 crewpeople. How many pairs of gloves would each crewperson receive. Dividing 24 by 8 yields 3; each crewperson would receive 3 pairs of gloves. Some words and symbols often seen in division are divided by, into, the symbol "÷",and the symbol "/". Just as multiplication is thought of as repeated addition, division can be thought of as repeated subtraction.

Some terms used in division include:
Divisor - the number by which a larger number is divided.
Dividend - the sum or amount to be divided and distributed.
Quotient - the number resulting from the division of one number by another .
Remainder - the number left after division that is smaller than the divisor.

In the equation b/a = c, b is the dividend, a is divisor, and c is the quotient.


Example 1- There are 20 nozzles for 5 engines. If the nozzles were to be divided evenly for the engines, how many nozzles would go on each engine?

20 - 5 = 15 - 5 = 10 - 5 = 5 - 5 =0. In this case, 5 was subtracted from 20 a total of 4 times. The answer to 20 divided by 5 is written as 20 ÷ 5 = 4
 

Example 2 - Divide 15 by 4.
15 - 4 = 11 - 4 = 7 - 4 = 3
Because 4 cannot be subtracted from 3, the 3 is called the remainder and is noted by the symbol "R".

The remainder is never larger than the divisor. The divisor in this example is 4. So, 15 / 4 = 3 R 3

If these were fifteen nozzles for four engines on your district, four nozzles would go on three engines and only three nozzles would go on the last engine. 
 

LONG DIVISION FOR LARGER NUMBERS

Long division can be used when working with larger numbers. Here the repeated subtraction is done in a different way. To divide, start from the digit of highest place value and finish with the digit in the lowest place value. At each step, ask if there are multiples of the number in the answer. 

Example 3 - Divide 3654 by 5.


Step 1. Start with the thousands digit in the number being divided. 5 is larger than 3, so move to the next step.

Step 2. Look at the hundreds place. Can 5 go into 36? Yes: 7 × 5 = 35. Fill in the ones and tens places with "0"s and subtract.

Step 4. Go to the tens place of the remainder (the number 154) that was subtracted in the previous step. Can 5 go into 15? Yes: 5 × 3 = 15. Fill in the "0" in the ones place and subtract

Step 5. Go to the ones place. Can 5 go into 4? No. 4 is smaller than 5. Put a "0" in the ones spot of the answer. There is a remainder of 4.

The answer to 3,654 ÷ 5 is written 730 R 4
To check the answer to this long division problem, multiply 730 × 5 to give 3,650. Adding the remainder of 4 gives 3654. The original dividend was 3654, so the answer is correct.
 

DIVIDING SIGNED NUMBERS

Dividing signed numbers follows the same general rules as multiplication. When dividing any two numbers having the same sign, the answer is positive, while that of two numbers of opposite sign is negative. When dividing numbers with like signs, the answer is positive. When dividing numbers with unlike signs, the answer is negative.
20 ÷ (-4) = -5
48 ÷ (-8) = -6
-100 ÷ (-10) = 10
-49 ÷ 11 = -4 R 5

DECIMAL NUMBERS

How a number is read depends on where the decimal point is placed. The figure below is similar to the chart for large numbers in Section 1.1. The decimal point comes after the ones position. The numbers to the right of the decimals represent tenths (0.1), hundreds (0.01), thousands (0.001), and so on down to infinitesimally small numbers.

All whole numbers (called integers) have a decimal point at the end. For instance, 10 = 10., 24 = 24., and 17,801 = 17,801 = 17,801.0.
 

 

MULTIPLES OF 10

Decimals correspond to multiples of 10. Note that the numbers 10, 100, 1000, 10,000 and so on are written similarly except for the number of "0"s between the first digit and the decimal point. This fact allows for division using these numbers to work by simply moving the decimal place. To divide by a factor of 10, count the number of zeros in the divisor or denominator and move the decimal point that many spaces to the left.

Consider 100/10, which can be written 100.0/10.0.

There is one zero in the 10, so move the decimal point in the 100 to the left by one place. 100/10 = 10.

Example 1 - Compute 8679 ÷ 1000. There are three zeros in 1000. Move the decimal point three places to the left, remembering that whole numbers have a decimal point at the end.

We can write 8679 ÷ 1000 = 8679. ÷ 1000. = 8.679
 

SIGNIFICANT FIGURES AND ROUNDING FOR ACCURACY

A decimal place indicates the accuracy of the given number. The accuracy of an answer is determined by the lowest level of accuracy of the original numbers being added, subtracted, multiplied, or divided. Accuracy does not improve with addition, subtraction, multiplication, or division. This detail is especially important for performing multiplication and division with decimal places.
 

Example 2 - What is 8.2 + 0.25? The lowest level of accuracy is to the 0.1 (or 1/10th) decimal place, so the correct answer is to the 1/10th decimal place. Rounding up or down is a method of bringing the answer to the correct level of accuracy. 8.2 + 0.25 = 8.45. However, the answer is only accurate to the 1/10th. What is 8.45 to the nearest 1/10th? To get the answer to the appropriate accuracy, round up or round down the digit beyond the lowest level of accuracy. If the number to be rounded is 5, 6, 7, 8, or 9, round up. Round down if the numbers are 4, 3, 2, or 1. 

For 8.2 + 0.25 = 8.45, round up the 0.45 to 0.5. The answer of 8.5 has the correct accuracy.
 

Example 3 - What is 986.525 minus 459.83? 

Performing the subtraction yields the result 526.695. The lowest level of accuracy is to the 0.01 (1/100ths) decimal place, so the digit in the 0.001 (1/1000ths) place must be rounded up or down. The last digit is a 5, so we round up and express the answer as 986.525 - 459.83 = 526.70.

When adding, subtracting, multiplying, or dividing digits, all numbers must have the same number of significant digits as the least accurate original number.

 

Example 4 - A helicopter landing pad is in the shape of the six-sided figure below. 
Side A is 12.50 feet long. 
Side B is 6.57 feet long. 
Side C is 7.8 feet long. 
Side D is 11.00 feet long. 
Side E is 5.5 feet long. 
Side F is 8.15 feet long. 
What is the total perimeter of the helicopter pad?



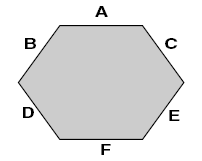
This problem involves adding numbers that are written using decimal notation.
First, set up the sum: 12.50 + 6.57 + 7.8 + 11.00 + 5.5 + 8.15 = 51.52

Now, check to see that your answer is expressed the correct accuracy. The lowest level of accuracy is the 0.1 (1/10ths) decimal place, as expressed by 7.8 and 5.5. Rounding the 0.01 (1/100ths) place digit, we express the perimeter of the helicopter pad as 51.5 feet.
 

MULTIPLICATION WITH DECIMALS

Accuracy in an answer is indicated by placement of the decimal point when multiplying numbers.

In multiplication, determine the correct decimal point after the multiplication is complete. After the numbers have been multiplied, count the number of places to the right of both of the original numbers. The lower amount of decimal places is then applied to the product as the number of places to the right of the decimal.

Example 5 - Multiply 0.9 × 1.53.


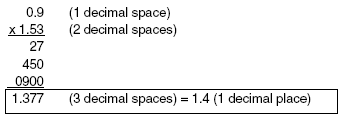
In this example, 1.377 has three decimal places, but the lowest accuracy number involved in the multiplication (0.9) has 0.1 (1/10ths) accuracy. Round the answer to the tenths place: 0.9 × 1.53 = 1.4

DIVISION WITH DECIMALS

When performing division, it is important to look at the dividend, which is the number that is being divided. Long division is performed by placing the decimal point in the answer directly above the decimal point in the number being divided.

Example 6 - Compute 89.76 ÷ 12



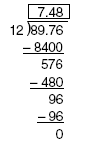
In this case, the answer 7.48 has the same number of decimal places as the dividend.

If the divisor is not a whole number, the decimal places need to be moved in both the divisor and dividend to make sure that the decimal in the quotient is correctly placed. First, move the decimal point in the divisor to the right to make the number into a whole number, or integer. Then, move the decimal point in the number being divided (the dividend) to the right by the same number of spaces. Now, place the decimal point directly above the point in the number being divided and divide as though dividing whole numbers.

Example 7 - Divide 4.067 / 0.83. 
To make the divisor a whole number, the decimal point must be moved two places to the right so the divisor becomes 83. The decimal point must also be moved in the dividend, so that the dividend becomes 406.7


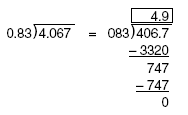
Now, long division proceeds as with whole numbers, and the answer to 406.7/0.83 is 4.9.

DOES YOUR ANSWER MAKE SENSE?

One tip for working with decimals is to ask yourself, "does that answer make sense"? If you are adding or multiplying whole numbers (integers), your end result should be larger then the numbers being multiplied. If you are subtracting or dividing whole numbers (integers), your result should be smaller. We can do a quick check of the division involving decimals in Example 7 by the looking the numbers being divided. In this case, we are dividing a number slightly larger than 4, by a number slightly smaller than 1. We can compute that 4 ÷ 1 is 4, so our number should be somewhat close to that. It should not be 40, or 0.4, or 400. In doing calculations in the field, look carefully at the numbers involved, and the operation (addition, multiplication, etc.). In many situations, the answer can be imperative to your safety, so make sure that the end result makes sense.

POWERS AND EXPONENTS

When a number is multiplied by itself several times, instead of writing each repetition of the multiplication, it is easier to use exponential notation. For example, 12 × 12 × 12 × 12 × 12 × 12 would be 12 multiplied to itself 6 times or 12⁶. The number being multiplied is called the base and the number of times it is multiplied by itself is called the exponent. In the above case, the base is 12 and the exponent is 6. When a number has an exponent of 2, it is said to be squared. When the exponent is 3, the number is said to be cubed. When the exponent is 4, the number is expressed as the base to the fourth power, and so on.

Example 1 - Write 6 × 6 × 6 in exponential notation and in words. Solve.

6 × 6 × 6 = "six cubed" or 6³. 6³ = 216.

SQUARE ROOT

Powers can also be worked backwards to find the square root of the number. The number whose root you want to find will appear under a square root sign: √x. The square root of a number x is the number that would have to be squared in order to get x.

For example, the square root of 4 would be 2, since 2² = 4.

Example 2 - Find √49

√49 = 7 because 7 × 7 = 49
 

Perfect squares are numbers having a square root that is an integer. Not all numbers are perfect squares. In these situations, divide to see whether the number can be separated into two factors: the first factor is a number that is a perfect square while the rest stays as a square root.

Example 3  - Find √18
Divide into √(9x2). The square root of 9 is an integer (3), so it can be taken outside of the square root symbol. The 2 remains under the square root symbol, because it is not a perfect square. √18 = 3 × √ 2.

ORDER OF OPERATION

Some math problems are a mixture of addition, subtraction, division, and multiplication. An operation to be performed might be true for one item but not another, so parentheses are used () for clarification.

There is a specific order to follow when making calculations.

The order in which operations are performed is:

1. Parentheses: ( )
2. Exponents: 2³
3. Multiplication and division
4. Addition and subtraction
5. Left to right

Note: It is always useful to add parentheses to clarify the order.

Example 1 - Solve 10 + 10 ÷ 10

Step 1. Division is performed before addition.
10 ÷ 10 = 1

Step 2. Add.
10 + 1 = 11

10 + 10 ÷ 10 = 11

The same example can be rewritten:
10 + 10 ÷ 10
10 + (10 ÷ 10). Using the parentheses helps clarify the order of operation.

Example 2 - Solve 6³ ÷ (10 - 8)² ÷ 2 + 2

Step 1. Parentheses.
6³ ÷ (10 - 8)² ÷ 2 + 2 = 6³ ÷ 2² ÷ 2 + 2

Step 2. Exponents.
216 ÷ 4 ÷ 2 + 2

Step 3. Division in order from left to right.
216 ÷ 4 = 54
54 ÷ 2 = 27

Step 4. Addition.
27 + 2 = 29

6³ ÷ (10 - 8)² ÷ 2 + 2 = 29 

FRACTIONS: BITS AND PIECES

Fractions are used often, for instance when adding leftover pails of foam or mixing gas and oil for chain saw fuel. Fractions allow the use of parts of a number or combinations of parts and whole numbers, such as  , , 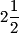or . The remainder found in long division can be changed to a fraction. Like whole numbers, fractions can be added, subtracted, divided, and multiplied. Fractions can also be represented as decimals (see Section 1.6).

A fraction consists of a numerator (top number) and a denominator (bottom number).

The numerator represents the number of parts available.

The denominator represents the number of parts in a whole.

Example 1 - What fraction of the box in the figure below is shaded? What fraction is not shaded?



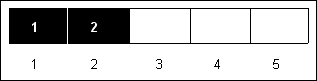
The box is divided into five parts. Two of those five parts are shaded. The shaded fraction represents 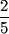. In this case,  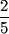of the figure is shaded.
Three of the five parts are not shaded. The unshaded fraction represents . In this case,  of the figure is not shaded.

WHOLE NUMBERS AS FRACTIONS

Fractions can also describe whole numbers or a whole number with a remainder expressed as a fraction. For example, a whole number can be written as: 

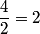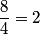, , or 

 

The whole number 1 can be written as:

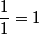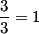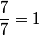, , , etc.

Fractions larger than 1 have a larger number in the numerator or top part of the fraction.

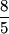, , and  are all larger than 1.

SIMPLIFYING FRACTIONS

Simplifying a fraction is writing a number in its most basic form. Sometimes fractions involve very large numbers in both the numerator (top number) and in the denominator (bottom number). As a general rule, it is easier to work with simpler fractions. So, always simplify.

There are three basic rules for simplifying fractions:

1. Any number written over 1 is that number.
2. A fraction can be simplified if the top and bottom numbers can both be divided by the same number, without leaving a remainder.
3. If the top number is larger than the bottom number, and neither number can be divided by the same number, divide the top number by the bottom number.

MULTIPLYING FRACTIONS

A whole number and a fraction, or two or more fractions, can be multiplied together. Whole numbers and fractions must be changed to all fractions, with no whole numbers, in order to multiply.

There are three steps to multiplying fractions:

1. Multiply the top numbers (numerators) by each other.
2. Multiply the bottom numbers (denominators) by each other.
3. Simplify the fraction (if possible).

DIVIDING FRACTIONS

Division of fractions involves using the reciprocal (flipped form) of the second fraction. The reciprocal of a number is such that the product of a number and its reciprocal is 1. To get the reciprocal, simply interchange (flip) the numerator and the denominator. 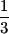 becomes ,  becomes , and so on.

After the second fraction has been flipped, the division problem turns into a multiplication problem, and the numerators and denominators are multiplied straight across.

ADDING FRACTIONS

There are three steps to adding fractions:

1. Ensure that the bottom numbers (denominators) are the same. If they are not, change them so that they are the same (they have a common denominator).
2. Once the denominators are the same, add the top numbers (nominators) and place the result over the common denominator.
3. Simplify the fraction (if possible).

SUBTRACTING FRACTIONS

Similar to adding fractions, fractions must have a common denominator (the bottom numbers must be the same) before being subtracted.

There are three steps to subtracting fractions:

1. Ensure that the bottom numbers (denominators) are the same. If they are not, change them so that they are the same (they have a common denominator).
2. Once the denominators are the same, subtract the top numbers (numerators) and place the result over the common denominator.
3. Simplify the fraction (if possible).

RATIOS

A ratio is a proportional relationship of one value to another, e.g., the ratio of gas to oil in chain saw mix. Ratios can be written either as a fraction, 1/2, or in ratio notation, 1:2. The value of a ratio is the division of the first number by the second number. For example, consider the ratio 1:40 . This ratio is read as "1 to 40". Any fraction, for instance, 1/20, can also be written as a ratio: 1:20

Example 1 - The Mara Bella District has 6 engines. The Baldy District has 5 engines. What is the ratio of engines in the Mara Bella versus the Baldy districts? 

The ratio of engines in the Mara Bella versus Baldy districts is 6:5 or 6/5.
 

PERCENTAGES

A percentage is another way of describing a ratio with respect to 100. Percent (%) is a value corresponding to how many out of a hundred (per hundred). For instance, if 92 out of 100 firefighters have completed the FireFighter Math course, the ratio of firefighters completing the course is 92:100, and the percentage is written as 92%.

Example 2 - Write four notations for 56.8%.

56.8% = 56.8 out of 100
56.8% = 56.8/100
56.8% = 56.8:100
56.8% = 0.568 (Note that performing this calculation results in moving the decimal two places to the left because there are two zeros in 100.)
 

PERCENTAGES AND LIVE FUEL MOISTURES

Percentages are useful for a number of fire science applications. One of these applications is estimating live fuel moisture. Live fuel moisture can be measured using oven drying and weighing procedures. Because this process is time-consuming and cannot be completed in the field, fire considerations are usually satisfied with a good estimate. Live fuel moisture can be estimated using the values in the figure below, which provides moisture percentages for fuels at different stages of vegetative development. For instance, from the figure, we observe that completely cured fuels have a live fuel moisture of less than 30%. This value is the result of subtracting the dry weight of the fuel from the total (wet) weight and dividing by the dry weight. 


 

Example 3 - A fuel sample collected in the field weighs 377 grams. After the sample is dried in an oven, it weighs 198 grams. What is the live fuel moisture content?

Step 1. Subtract the dry weight from the wet weight. 377 - 198 = 179.

Step 2.Divide the difference by the dry weight and multiply by 100 to find the value as a percent. 179 / 198 × 100 = 0.904 × 100 = 90.4%. 

The live fuel moisture of your sample is 90.4%. 
 

PROBLEM SOLVING WITH RATIOS

When solving a more complex percentage or ratio problem, write the problem down in words and numbers and work through one step at a time.